При дизайне, запуске и анализе A/B тестов можно допустить много ошибок, но одна из них особенно коварна. Речь о «peeking problem» или «проблеме подглядывания», когда решение об изменениях в продукте принимается на основе промежуточных результатов теста.
Эту ошибку допускают и те, у кого много опыта в A/B тестировании и кто понимает, как оценить статистическую значимость наблюдаемых изменений.
В этом материале мы разберем, зачем измерять статистическую значимость и как проблема подглядывания мешает правильному анализу результатов эксперимента.
Если вы хотите глубже разобраться в том, как создаются, развиваются и масштабируются продукты, пройдите обучение в симуляторах GoPractice.
→ «Симулятор управления продуктом на основе данных» поможет научиться принимать решения с помощью данных и исследований при создании продукта (путь от 0 к 1).
→ «Симулятор управления ростом продукта» поможет найти пути управляемого роста и масштабирования продукта. Вы построите модель роста и составите стратегию развития продукта (путь от 1 к N).
→ «Симулятор SQL для продуктовой аналитики» поможет освоить SQL и применять его для решения продуктовых и маркетинговых задач.
→ «Симулятор управления ML/AI-проектами» научит применять технологии машинного обучения с пользой для бизнеса.
Не знаете с чего начать? Пройдите бесплатный тест для оценки навыков управления продуктом. Вы определите свои сильные стороны и слепые зоны, получите план профессионального развития.
Еще больше ценных материалов и инсайтов — в телеграм-канале .
Статистическая значимость простыми словами
Представим, что вы привлекли в игру 10 новых пользователей и случайно разделили их между старой и новой версией. Из 5 пользователей, которые попали в старую версию игры, на следующий день вернулись 2 (40%). Из 5 пользователей, которые попали в новую версию, на следующий день вернулись 3 (60%).
Можно ли на основе собранных данных сказать, что Retention 1 дня новой версии игры лучше, чем старой?
К сожалению, нельзя. Выборка очень маленькая, поэтому велика вероятность, что наблюдаемая разница — случайность, а не результат изменений.
Математическая статистика предоставляет инструменты, помогающие понять, можно ли различия в метрике между группами связать с изменениями продукта, а не со случайностью. Другими словами, является изменение статистически значимым или нет.
Способ проверки статистической значимости в рамках частотного подхода к теории вероятности, которому обычно учат в университетах, работает следующим образом:
- Собираются данные для версии A и B.
- Делается предположение, что тестовые группы между собой не отличаются.
- В рамках предположения идентичности групп считается, какова вероятность получить наблюдаемую в эксперименте или большую разницу между группами. Такое значение называют p-value.
- Если p-value меньше определенного порогового значения (обычно 5%), то изначальное предположение об идентичности тестовой и контрольной группы отвергается. В этом случае можно с высокой степенью уверенности утверждать, что наблюдаемая разница между группами значима (связана с их различиями, а не случайностью).
- Если p-value больше порогового значения, то тестируемые версии на основе собранных данных неразличимы. При этом в реальности между ними как может быть различие, которое мы просто не выявили, так его может и не быть. Мы не знаем.
Это очень поверхностное объяснение основной идеи того, как и зачем считать статистическую значимость. В реальности все сложнее: необходимо изучить структуру данных, очистить их, выбрать правильный критерий, интерпретировать результаты. Все эти шаги таят в себе много подводных камней.
Простой пример расчета статистической значимости
Давайте вернемся к игре из прошлого примера.
Команда учла недостатки дизайна первого A/B теста и на этот раз привлекла 2000 новых пользователей (по 1000 в каждую из версий). На 1 день в первой версии вернулись 330, а во второй 420.
Во второй версии больше пользователей вернулись на 1 день, но команда не могла быть уверена, что это произошло из-за влияния продуктовых изменений, а не в результате случайного колебания метрики.
Для разрешения вопроса надо было посчитать, является ли наблюдаемая разница в Retention 1 дня статистически значимой или нет.
В данном случае изучалась простая метрика (конверсия новых пользователей в определенное действие — возвращение на 1 день), поэтому можно было воспользоваться для расчета статистической значимости.
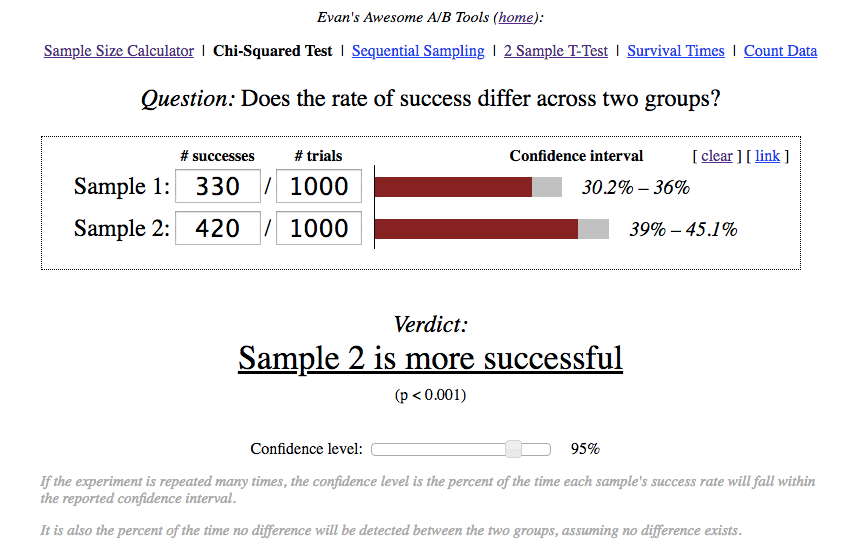
Калькулятор выдал p-value < 0.001, то есть вероятность увидеть наблюдаемое различие при идентичных тестовых группах очень мала. Значит, можно с высокой степенью уверенности связать рост Retention 1 дня с влиянием продуктовых изменений.
Автоматизация проверки результатов A/B теста c неожиданными последствиями
Команда, воодушевленная прогрессом с Retention, решила переключиться на улучшение монетизации игры. Сначала там решили сфокусироваться на увеличении конверсии в первую покупку. Спустя 2 недели новая версия игры ушла в A/B тест.
Разработчики проявили инициативу и написали скрипт, который каждые несколько часов считал конверсию в первую покупку для тестовой и контрольной версии и проверял, является ли разница значимой.
Спустя несколько дней система выдала сообщение о наличии значимой разницы. Эксперимент признали успешным и новую версию раскатили на всех пользователей.
Вы могли не заметить, но в процесс анализа эксперимента закралась коварная ошибка.
Peeking problem или проблема подглядывания
Применение стандартных критериев в рамках частотного подхода к статистике (Хи-квадрат, критерий Стюдента), которые используются для расчета p-value и статистической значимости, требуют выполнения различных условий. Например, многие критерии подразумевают нормальное распределение изучаемой величины.
Но есть еще одно важное условие, о существовании которого многие забывают: размер выборки для эксперимента должен быть определен заранее.
Вы должны заранее решить, сколько наблюдений хотите собрать. Потом посчитать результаты и принять решение. Если вдруг выявить значимую разницу на собранном количестве данных не получилось, то продолжать эксперимент с целью сбора дополнительных наблюдений нельзя. Можно только запустить тест заново.
Описанная логика звучит странно в контексте A/B тестов в интернете, где можно смотреть на результаты в режиме реального времени, где добавление новых пользователей в эксперимент ничего не стоит.
Дело в том, что используемый для A/B тестов математический аппарат в рамках частотного подхода к статистике разрабатывался задолго до появления интернета. Тогда большинство прикладных задач подразумевало фиксированный и заранее определенный размер выборки для проверки гипотезы.
Интернет поменял парадигму A/B тестирования. Вместо выбора фиксированного размера выборки перед запуском эксперимента большинство предпочитают собирать данные, пока разница между тестом и контролем не станет значимой. Следствием такого изменения в процедуре проведения экспериментов стало то, что расчеты p-value старыми способами перестали работать. Реальное p-value при регулярной проверке результатов теста становится намного больше, чем то p-value, который вы получаете, используя обычные статистические критерии, которые при такой процедуре перестают работать.
Проблема подглядывания проявляется, когда вы проверяете промежуточные результаты с готовностью принять решение: раскатить одну из версий, если различие между тестом и контролем окажется значимым. Если вы зафиксировали размер выборки и просто наблюдаете за результатами в процессе набора наблюдений (и ничего не делаете на их основе), а потом принимаете решение, когда набралось нужное количество данных, то никаких проблем не возникает.
Правильная процедура A/B тестирования (в рамках частотного подхода):
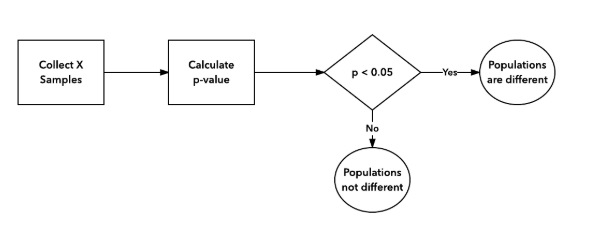
Неправильная процедура A/B тестирования:
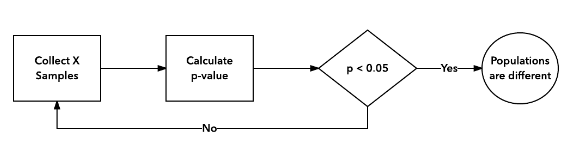
Почему подглядывания увеличивают p-value
Давайте вернемся к эксперименту про конверсию в первую покупку в игре. Предположим, мы знаем, что в реальности сделанные изменения не оказали никакого влияния.
Ниже изображена динамика разницы конверсий в покупку между тестовой и контрольной версиями продукта (синяя линия). Зеленая и красная линия отражают границы диапазона неразличимости при условии, что заранее было выбрано соответствующее количество наблюдений.
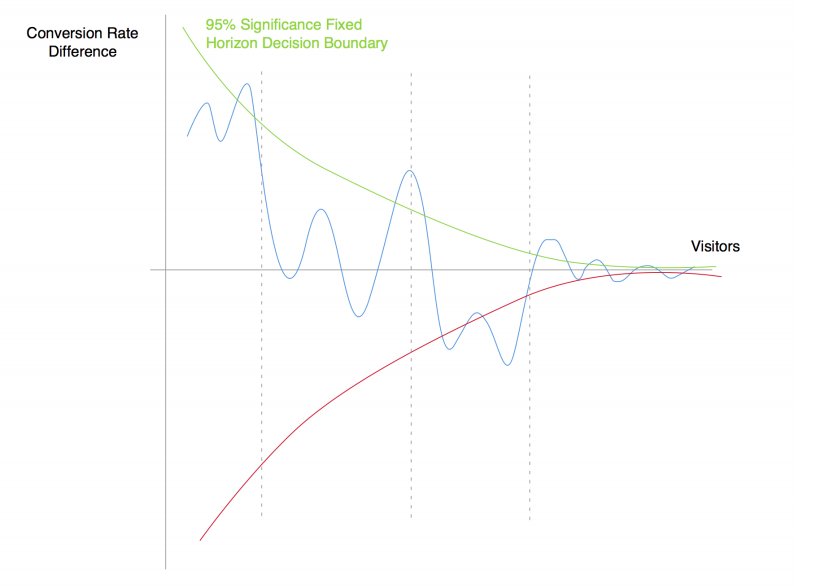
При правильном процессе A/B тестирования надо заранее определить количество пользователей, на основе которых будет оцениваться результат, собрать наблюдения, посчитать результаты и сделать вывод. Такая процедура гарантирует, что при многократном ее повторении в 95% случаев критерий не увидит разницы между одинаковыми версиями (при соответствующем уровне доверия).
Все меняется, если вы начинаете проверять результаты с определенной частотой и готовы действовать на основе наблюдаемых различий. В таком случае вместо вопроса о том, является ли разница значимой в определенный заранее выбранный момент в будущем, вы спрашиваете, выходит ли разница за диапазон неразличимости хотя бы раз в процессе сбора данных. Это два совершенно разных вопроса.
Даже если две группы идентичны, то разница конверсий может периодически выходить за границы зоны неразличимости по мере накопления наблюдений. Это совершенно нормально, так как границы сформированы так, чтобы при тестировании одинаковых версий лишь в 95% случаев разница оказывалась в их пределах.
Поэтому при регулярной проверке результатов в процессе проведения теста с готовностью принять решение при наличии значимой разницы вы начинаете кумулятивно накапливать возможные случайные моменты, когда разница выходит за пределы диапазона. Следствие — p-value растет с каждой новой проверкой.
Вот того, как именно подглядывания увеличивают p-value.
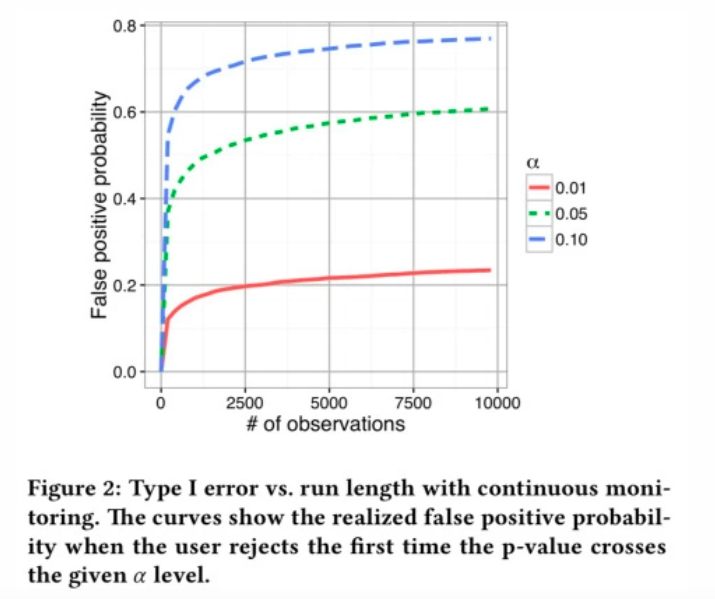
Влияние подглядываний на p-value
Чем чаще вы смотрите на промежуточные результаты A/B теста с готовностью принять на их основе решение, тем выше становится вероятность, что критерий покажет значимую разницу, когда ее нет:
- 2 подглядывания с готовностью принять решение о завершении теста увеличивают p-value в 2 раза;
- 5 подглядываний в 3.2 раза;
- 10 000 подглядываний более чем в 12 раз.
Варианты решения проблемы подглядывания
Фиксировать размер выборки заранее и не проверять результаты, пока все данные не собраны
Очень правильный и очень непрактичный подход. Если эксперимент не даст никакого сигнала, то придется все начинать заново.
Математические пути решения проблемы: Sequential experiment design, байесовский подход к A/B тестированию, снижение чувствительности критерия
Проблема подглядывания может быть решена математическим путем. Например, Optimizely и Google Experiments используют для ее решения микс байесовского подхода к A/B тестированию и . Рассуждения выше мы вели в рамках частотного подхода, подробнее о разнице байесовского и частотного подходов — по ссылкам в конце статьи.
Для сервисов вроде Optimizely — это необходимость, так как их ценность сводится к тому, что они определяют лучший вариант на основе регулярной проверки результатов A/B теста на лету. Подробнее можно почитать по следующим ссылкам: , .
Продуктовый подход с мягким обязательством по времени теста и коррекцией на суть проблемы подглядывания
При работе над продуктом ваша цель — получить сигнал, необходимый для принятия решения. Описанная ниже логика неидеальна с математической точки зрения, но решает продуктовую задачу.
Суть подхода сводится к тому, чтобы предварительно оценить необходимую выборку для выявления эффекта в A/B тесте и учесть природу проблемы подглядывания в процессе промежуточных проверок. Это позволяет минимизировать негативные последствия при анализе результатов.
Перед стартом эксперимента стоит оценить, какая нужна выборка, чтобы с приемлемой вероятностью увидеть изменение, если это изменение в реальности есть.
Это полезное упражнение безотносительно проблемы подглядывания, так как для некоторых продуктовых фич требуется столь большая выборка, чтобы идентифицировать их эффект, что тестировать их на текущем этапе развития продукта нет смысла.
Держа в уме посчитанную ранее выборку, после запуска эксперимента можно (и даже нужно) следить за динамикой изменений, но не принимать решений, при первом выходе разницы в зону значимости.
Нужно продолжать наблюдать. Если разница зафиксируется, то, скорее всего, влияние есть. Если же станет вновь неразличимой, то сделать однозначного вывода об улучшении нельзя.
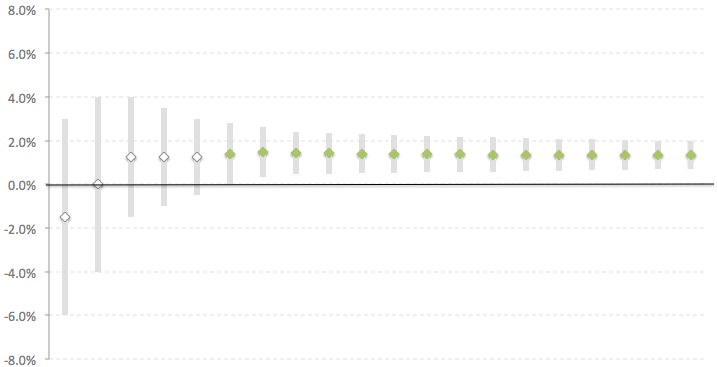
Давайте посмотрим на результаты двух экспериментов ниже. Оба эксперимента шли 20 дней, каждая точка на графике — относительная разница в метрике между тестом и контролем на конец соответствующего дня с доверительным интервалом. Если доверительный интервал не пересекает ноль (идентично выполнению условия p-value < x), то разница является значимой (при выборе соответствующей выборки заранее). В этом случае точка выделяется зеленым.
В первом эксперименте, начиная с 6 дня, разница между версиями стала значимой и доверительный интервал больше не пересекал 0. Такая устойчивая картина дает четкий сигнал о том, что с высокой степенью вероятности тестовая версия работает лучше контрольной. Сложностей с интерпретацией результатов нет.
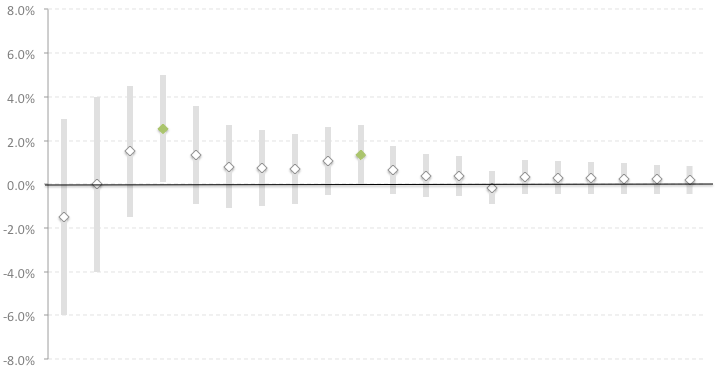
Во втором эксперименте разница иногда выходила в зону значимости, но потом вновь становилась неразличимой. Если бы мы не знали о проблеме подглядывания, то мы закончили бы эксперимент на 4 день, решив, что тестовая версия выиграла. Но предложенный способ визуализации динамики A/B теста во времени показывает, что устойчивой измеримой разницы между группами нет.
Возможны пограничные случаи, когда однозначно интерпретировать результаты сложно. Единого способа их разрешения нет, все зависит от рискованности и стоимости принимаемого решения.
- Есть обычные эксперименты, где вы тестируете разные реализации фичи или небольшие изменения, и готовы принимать решение с большей степенью риска.
- Есть дорогие решения, когда вы, например, пытаетесь проверить новый вектор развития продукта. В этом случае стоит уделить анализу и изучению данных больше времени. Иногда можно провести эксперимент еще раз.
Описанная логика может звучать как излишнее упрощение с точки зрения математики, но для продуктовой работы она вполне подходит. Когда в продуктовой работе начинают больше заниматься математикой, чем продуктом, то обычно дело в том, что эффект от изменений слишком мал или отсутствует, а эту проблему математикой не решить.
В заключение
Ключевая мысль этого материала такова:
Если вы проводите A/B тест и в определенный момент разница стала значимой, то не надо сразу заканчивать эксперимент, считая, что одна из групп выиграла. Продолжайте наблюдать. А лучше заранее выберите размер выборки, соберите наблюдения, а потом на их основе посчитайте результаты.
Дополнительное чтение
- Хорошая про peeking problem.
- Еще одна хорошая про проблему подглядывания, но с ошибочным утверждением, что использование байесовского подхода ее решает.
- байесовского и частотного (frequentist) подходов простым языком.
- Математическим про разницу байесовского и частотного подходов.
- Наглядное , что байесовский подход к A/B тестам не решает проблему подглядывания от команды Stack Exchange.
- Еще одна про то, что байесовский подход чувствителен к подглядываниям, а также о том, как проблему решают разные сервисы A/B тестов на рынке.
- Обсуждение плюсов и минусов bayesian vs frequentist подходов к математической статистике на .
- про их подход решению проблемы подглядывания.
- Много интересного про Sequential анализ для A/B тестов — , и .
- про то, как растет p-value при мониторинге результатов с готовностью принять решение.
Если вы хотите глубже разобраться в том, как создаются, развиваются и масштабируются продукты, пройдите обучение в симуляторах GoPractice.
→ «Симулятор управления продуктом на основе данных» поможет научиться принимать решения с помощью данных и исследований при создании продукта (путь от 0 к 1).
→ «Симулятор управления ростом продукта» поможет найти пути управляемого роста и масштабирования продукта. Вы построите модель роста и составите стратегию развития продукта (путь от 1 к N).
→ «Симулятор SQL для продуктовой аналитики» поможет освоить SQL и применять его для решения продуктовых и маркетинговых задач.
→ «Симулятор управления ML/AI-проектами» научит применять технологии машинного обучения с пользой для бизнеса.
Не знаете с чего начать? Пройдите бесплатный тест для оценки навыков управления продуктом. Вы определите свои сильные стороны и слепые зоны, получите план профессионального развития.
Еще больше ценных материалов и инсайтов — в телеграм-канале .










