Среднее арифметическое и медиана — два способа оценить средние значения, часто используемые в продакт-менеджменте. В этом материале мы обсудим, чем эти способы различаются и когда какой из них лучше применять.
Это перевод из англоязычного блога GoPractice. При желании вы можете изучить его в оригинале
Среднее арифметическое
Среднее арифметическое — широко используемая мера центральной тенденции в анализе данных. Оно рассчитывается путем сложения всех значений в наборе данных и деления суммы на общее количество значений. Формула для среднего арифметического выглядит следующим образом:
Среднее арифметическое = (Сумма всех значений) / (Общее количество значений).
Допустим, вы продакт-менеджер интернет-магазина и вы хотите рассчитать среднюю стоимость корзины покупок за предыдущий день. Для начала вы соберете данные обо всех заказах за этот период времени, затем сложите стоимость всех заказов и разделите результат на количество значений. Пример может выглядеть так:
Средняя стоимость корзины покупок = ($45 + $32 + $56 + $78 + $23) / 5 = $46,80
Развивайтесь в профессии продакт-менеджера с помощью GoPractice.
→ «Профессия: продакт-менеджер».
→ «Симулятор управления продуктом на основе данных».
→ «Симулятор управления ростом продукта».
→ «Симулятор SQL для продуктовой аналитики»
→ «Симулятор управления ML/AI-проектами».
→ «Генеративный AI для продакт-менеджеров: мини-симулятор».
→ Не знаете с чего начать? Пройдите бесплатный тест для оценки навыков управления продуктом и подпишитесь на телеграм-канал .
Сильные стороны использования среднего арифметического в продакт-менеджменте
- Формулу среднего арифметического легко запомнить, она проста для понимания и вычисления. Ее удобно использовать в коммуникации со стейкхолдерами, которые могут не обладать глубокими знаниями в области статистики.
- Среднее арифметическое учитывает все значения в наборе данных.
- Среднее арифметическое — интуитивно понятная метрика, которая широко используется во многих областях. Она позволяет легко сравнивать различные наборы данных.
Слабые стороны использования среднего арифметического в продакт-менеджменте
- Среднее арифметическое очень чувствительно к так называемым «выбросам» — отдельным значениям, которые значительно отличаются от других в этом датасете, в большую или меньшую сторону. «Выбросы» могут искажать среднее значение, давая тем самым неверное представление о центральной тенденции в данных. В продакт-менеджменте опора на такие результаты может привести к неверным решениям или упущенным возможностям.
Например, продакт-менеджер решил проанализировать среднее время, которое люди проводят на его платформе для онлайн-обучения. Большинство пользователей проводит на ней около 30 минут, но небольшая часть из них проводят пять часов и более. Если продакт-менеджер будет полагаться только на среднее арифметическое, то получит сильно завышенное время пользовательских сессий. - Среднее арифметическое может оказаться слишком дорогим для вычисления, если речь идет о больших датасетах. Добавление всех значений в датасет требует времени, а для наборов данных с миллионами значений подсчет вручную будет нецелесообразным.
Сценарии применения среднего арифметического в продакт-менеджменте
Среднее арифметическое пригодится, когда требуется простая, интуитивно понятная метрика, которая представляет собой типичное значение для набора чисел без заметных «выбросов».
Этот показатель будет удобным при подсчете индекса удовлетворенности пользователей. Используя среднее арифметическое, вы можете дать равный вес всем оценкам, получить средний уровень удовлетворенности клиентов и затем отслеживать изменения показателя со временем.
Другой пример — подсчет стоимости установки мобильного приложения (CPI, cost per install). Рассчитав среднюю стоимость одной конверсии, вы получите обобщенные данные экономической эффективности приложения по многим конверсиям. Это поможет определить зоны роста, оптимизировать рекламные расходы и улучшить стратегию привлечения пользователей в целом.
Медиана
Медиана — это мера центральной тенденции, которая представляет собой серединное значение набора данных, расположенного в порядке от меньшего к большему. Медиана — полезный инструмент для анализа данных, когда в нем присутствуют «выбросы» или экстремальные значения, которые могут исказить среднее арифметическое.
Для расчета медианы нужно расположить значения в наборе данных от наименьшего к наибольшему. Если в наборе данных нечетное количество значений, медианой будет серединное значение.
Например, в наборе данных {3, 7, 12, 16, 19} медианой будет 12.
Если набор данных состоит из четного количества значений, то медиана — это среднее двух серединных значений.
Например, в наборе данных {4, 6, 10, 13, 18, 22} медиана будет равна (10 + 13) / 2 = 11,5.
Сильные стороны использования медианы в продакт-менеджменте
Медиана менее чувствительна к выбросам, чем среднее арифметическое, и более устойчива к влиянию нескольких экстремальных значений. В продуктовой работе медиана используется для анализа данных, содержащих экстремальные значения.
Например, если продакт-менеджер анализирует стоимость товаров в интернет-магазине, среди которых встречаются несколько очень дорогих позиций, то медиана отразит более близкие к реальности центральные тенденции в данных.
Медиану легче посчитать для больших датасетов, особенно если база данных проиндексирована и отсортирована правильно. Это может быть полезно для продактов, которым необходимо быстро и эффективно анализировать большие объемы данных. Например, при анализе времени отклика веб-сайта с миллионами пользователей найти медианное значение будет быстрее и эффективнее, чем считать среднее арифметическое.
Слабые стороны использования медианы в продакт-менеджменте
- Медиана может оказаться контринтуитивной для людей, которые слабо знакомы со статистикой. Например, это может осложнить донесение информации о данных до стейкхолдеров, которые не погружены в эту область.
- Медиана игнорирует некоторые значения в наборе данных, фокусируясь только на серединном значении. Это может создать сложности в ситуациях, когда важно учитывать все значения в наборе данных.
- Медиана не дает никакой информации о разбросе данных или о том, насколько изменчивы эти значения.
Например, продакт-менеджер анализирует время, которое пользователи проводят в продукте. Полагаясь только на медиану, он может упустить ценные инсайты о том, как варьируется вовлеченность пользователей. Например, если медианное время в продукте составляет 10 минут, это может свидетельствовать о высокой вовлеченности пользователей в продукт. Однако одна лишь медиана не дает никакой информации о том, сколько пользователей проводят в продукте очень мало или очень много времени. Также медиана не показывает, как вовлеченность варьируется в зависимости от демографических характеристик или поведения пользователя. Для продакта это может быть очень ценным знанием.
Примеры использования медианы в продакт-менеджменте
В целом, медиана — это полезный инструмент в тех случаях, когда экстремальные значения могут исказить среднее арифметическое. Это особенно важно в ситуациях, когда «выбросы» или экстремальные значения могут иметь существенное влияние на измерение показателей продукта или пользовательского опыта.
Пример оптимального использования медианы — анализ выручки с одного пользователя. В таком случае продакт может получить более точное значение, которое не искажено высокими показателями небольшого количества пользователей. Это полезно для составления достоверных прогнозов о доходах продукта.
Как выбрать между средним арифметическим и медианой
Несколько советов о том, как выбрать, использовать ли среднее арифметическое или медиану в каждом конкретном случае.
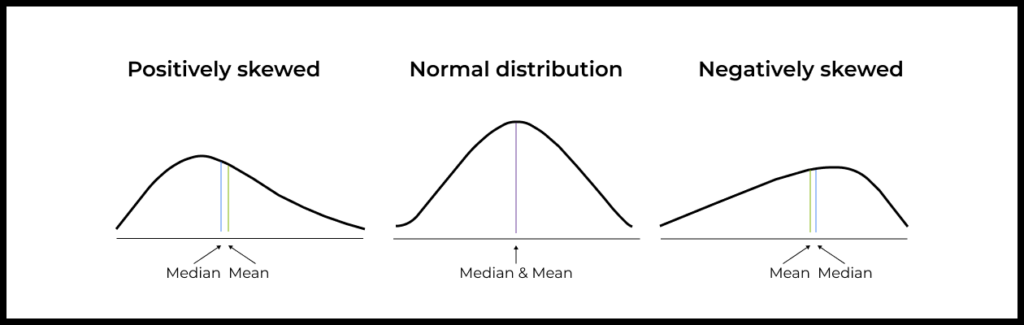
Распределение данных: если в датасете наблюдается нормальное распределение, то среднее арифметическое — хороший выбор для измерения центральной тенденции. Но если в данных есть «выбросы», то лучше использовать медиану.
Цель или контекст анализа: выбор между средним арифметическим и медианой может зависеть от контекста конкретного анализа. Например, для вычисления средней зарплаты группы людей лучше подойдет медианное значение. А когда речь идет о среднем весе (например, у пользователей приложения для здоровья), то лучшим выбором будет среднее арифметическое.
Размер выборки: если в вашем распоряжении небольшая выборка, то использовать стоит медиану, поскольку она менее чувствительна к «выбросам». В случае с большой выборкой среднее арифметическое будет более точно отражать реальность.
Совместное использование среднего арифметического и медианы
В ряде случаев использование среднего арифметического и медианы может дать более полную картину о центральных тенденциях в датасете. Анализируя обе метрики, продакт-менеджеры могут лучше понимать распределение значений и находить «выбросы» или экстремальные значения, которые могут оказывать влияние на данные.
Например, если продакт анализирует время, необходимое пользователю для решения задачи в приложении, полезно использовать обе метрики. Если среднее арифметическое времени значительно выше медианного, это может сигнализировать о том, что часть пользователей решает задачу дольше остальных. Значит, эти пользователи могли столкнуться с какими-то трудностями в продукте. Анализ обеих метрик поможет продакту увидеть такие «выбросы» в данных и идентифицировать возможные проблемы.
Роль данных в продуктовой работе растет, и для продакт-менеджеров возрастает ценность знаний в статистике и мерах центральной тенденции. Грамотное использование таких метрик позволяет продакт-менеджеру принимать решения на основе более полной и точной картины происходящего в продукте.
