A/B-тесты — важный инструмент в арсенале продуктовой команды. Это один из немногих способов понять, как изменения в продукте повлияли на поведение пользователей.
При этом любой человек, который погружается в тему A/B-тестов, сталкивается с двумя противоречивыми утверждениями:
Первое: t-тест — самый популярный критерий для оценки A/B-тестов.
Второе: t-тест можно применять только на данных, распределенных нормально.
Однако нормально распределенные данные в продуктах встречаются крайне редко.
В таком случае, что же делать, когда наши данные не подчиняются нормальному распределению? Можем ли мы все же полагаться на традиционные статистические методы (в частности, на t-тест), или нужно использовать другие методы, например бутстрап или непараметрические тесты?
В этом материале — ответ на этот вопрос и универсальный алгоритм для подбора подходящего статистического теста для ваших данных.
Этот материал совместно с GoPractice написал участник сообщества, Senior Product Analyst .
Если вам тоже интересно поучаствовать в создании публикаций для GoPractice, то оставляйте заявку на этой странице.
Далее — текст от лица автора.
***
Что такое t-тест?
T-тест — это статистический метод для определения того, есть ли значимая разница между средними двух выборок. Он вычисляет t-статистику с учетом разницы между средними, вариабельности и размеров выборок, после чего сравнивает ее с теоретическим распределением для получения p-value.
Прикладная применимость t-тестов
На самом деле t-тест прекрасно справляется с оценкой практически любых распределений данных при наличии большого количества данных.
Заблуждение же о его неприменимости для не нормально распределенных данных основывается на двух моментах:
1. Требования для нормального распределения является обязательным для небольшого количества наблюдений (несколько десятков).
В продуктовой сфере эксперименты обычно проводятся если не сотнях тысяч, то уж точно на тысячах пользователей. В статьи продуктовой тематики требование о нормальности перекочевало из медицинских источников, где в экспериментах обычно мало наблюдений: в группе может быть и десяток испытуемых.
2. Чтобы тест отработал как надо, распределение выборочных средних* должно быть нормальным.
Распределение выборочных средних подразумевает, что мы берем много случайных выборок из одних и тех же данных, считаем среднее для каждой выборки и смотрим, как эти средние распределяются.
Нормальное распределение выборочных средних гарантирует центральная предельная теорема (ЦПТ) при достаточно больших выборках. Кратко обозначим основные требования ЦПТ, которые обычно выполняются в продуктовых экспериментах:
- Независимость наблюдений. Поведение одного пользователя не влияет на другого.
- Одинаковое распределение. Пользователи взяты из одной генеральной совокупности (например, все — посетители одного продукта).
- Большой размер выборки. В продуктах обычно тысячи и даже миллионы наблюдений, что с запасом покрывает требуемый минимум (n ≥ 30 даже для не нормальных данных).
- Конечная дисперсия. Практически всегда выполняется, так как реальные продуктовые метрики редко имеют бесконечную дисперсию.
Таким образом, в реальных продуктовых условиях эти требования чаще всего легко удовлетворяются.
* Важно: нормально должны быть распределены именно выборочные средние, а не сама выборка.
Практическая проверка эффективности t-теста на разных распределениях
Мнения аналитиков по поводу того, когда и какой тест применять, расходятся довольно сильно. Тем не менее t-тест остается одним из самых популярных статистических критериев, используемых на практике.
Давайте проведем практическое исследование, чтобы доказать его эффективность.
Что мы будем делать
Для начала сгенерируем данные для теста из разных распределений (нормальное, одномодальное, логнормальное) с заранее заданными параметрами.
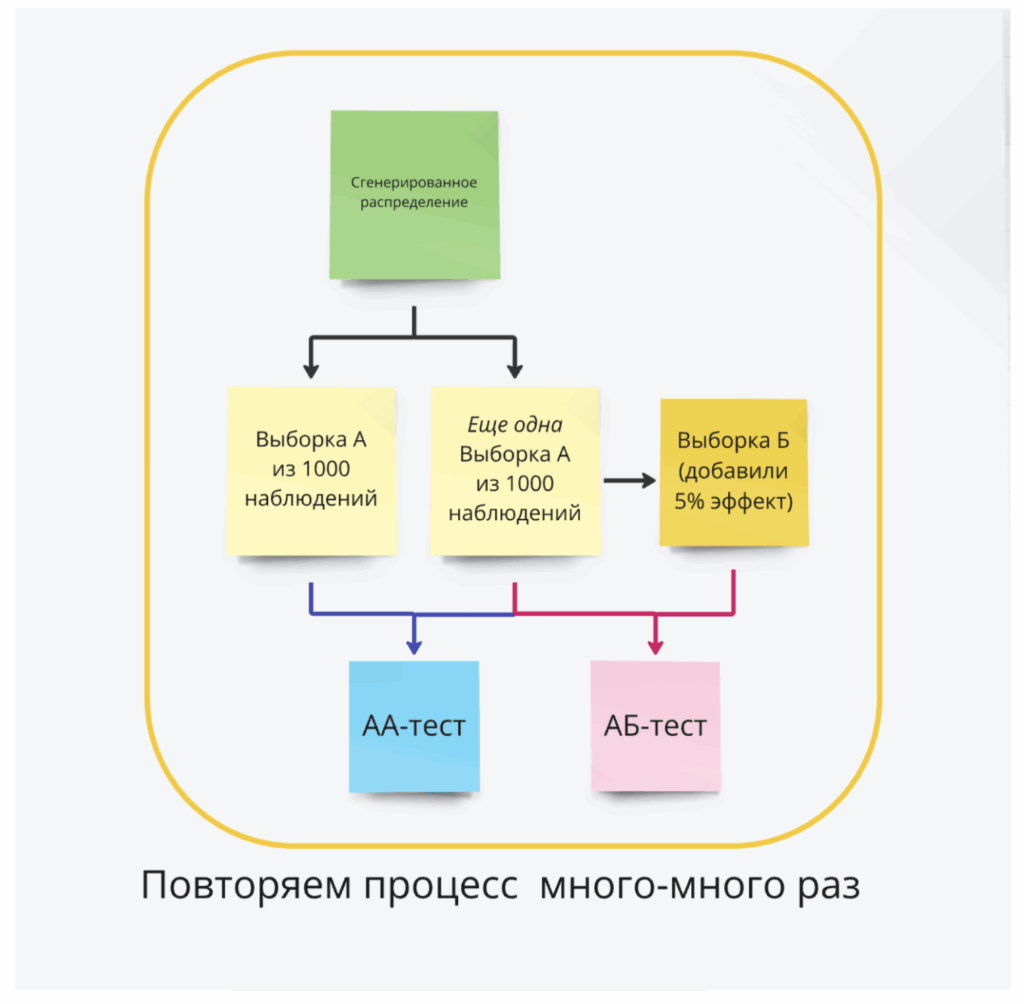
Далее — много раз (в нашем случае — 200) повторим следующий процесс:
Симуляция A/A-теста:
- Из каждого распределения будем брать две выборки по 1000 наблюдений. Так как обе выборки из одного распределения, мы точно знаем, что разницы между ними нет.
- Эти выборки мы будем использовать для симуляции A/A-теста: для каждой выборки посчитаем метрики (например, среднее), а затем сравним их между собой с помощью статистического теста.
Симуляция A/B-теста:
- Затем для одной из изначальных выборок данных добавим небольшой эффект (например, умножим все значения на 1.05, чем увеличим среднее значение метрики на 5%, что соответствует незначительному, но практически важному изменению поведения пользователей).
- Сравним выбранную метрику (среднее) между группами, симулируя проведение A/B-теста.
A/A-тесты используются для проверки корректности работы статистического критерия:
- Так как мы точно знаем, что в A/A-тесте разницы между группами нет, то все результаты со статзначимой разницей будут являться ложноположительными (статистический тест сказал, что разница есть, хотя ее в реальности нет).
- Процент ложноположительных тестов должен быть равен установленному уровню значимости теста (также его называют «альфа»). Уровень значимости вы выбираете сами при использовании статистического критерия; он определяет, с какой вероятностью мы ошибочно найдем эффект там, где его нет (обычно это значение равно 5%).
При этом в A/B-тесте все статзначимые результаты будут означать обнаружение реального эффекта (мы же ведь заложили разницу между группами в 5%):
- Поскольку мы добавили разницу в 5%, ожидается, что мощность теста (1 — β) определит, в каком проценте случаев тест правильно выявит этот эффект.
- Чем выше мощность, тем больше реальных эффектов мы сможем выловить с помощью А/Б теста — и тем меньше будет вероятность пропустить реальный эффект, когда он есть (ошибка II рода).
В итоге, сравнивая результаты A/A- и A/B-тестов, мы сможем оценить, насколько хорошо t-test работает на реальных данных с разным распределением.
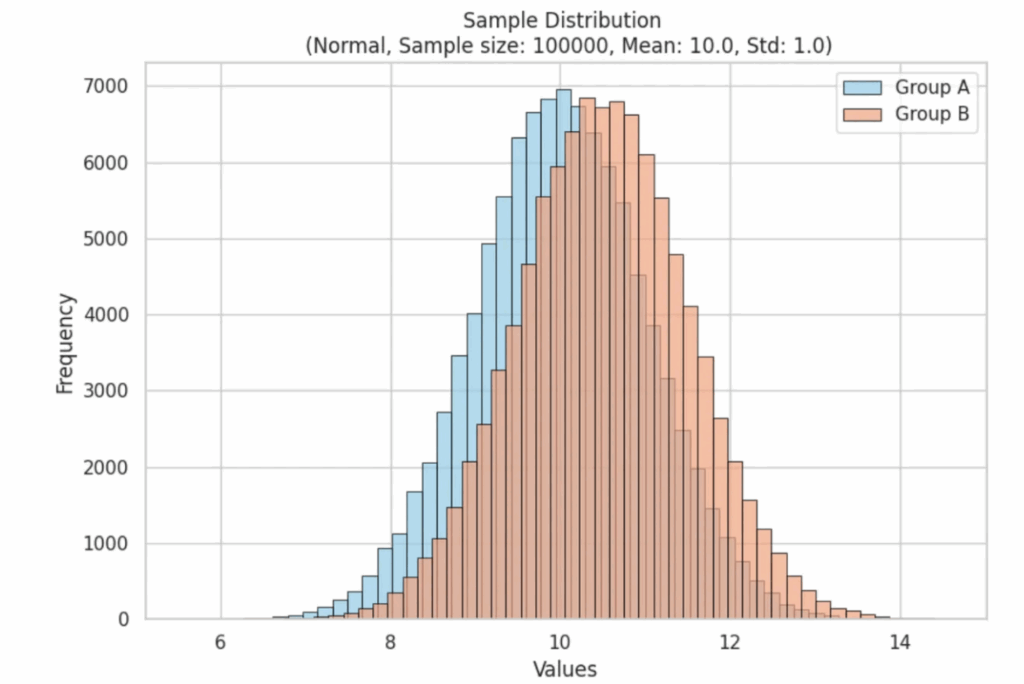
Сначала — нормальное распределение
Начнем с нормального распределения данных. На графике ниже исходное нормальное распределение обозначено голубым цветом, а оранжевым — аналогичное распределение, у которого среднее значение увеличено на 5%
Возьмем по 1000 случайных значений из каждой группы, посчитаем среднее для каждой выборки. Повторим 200 раз. У нас получится распределение выборочных средних для каждой группы:
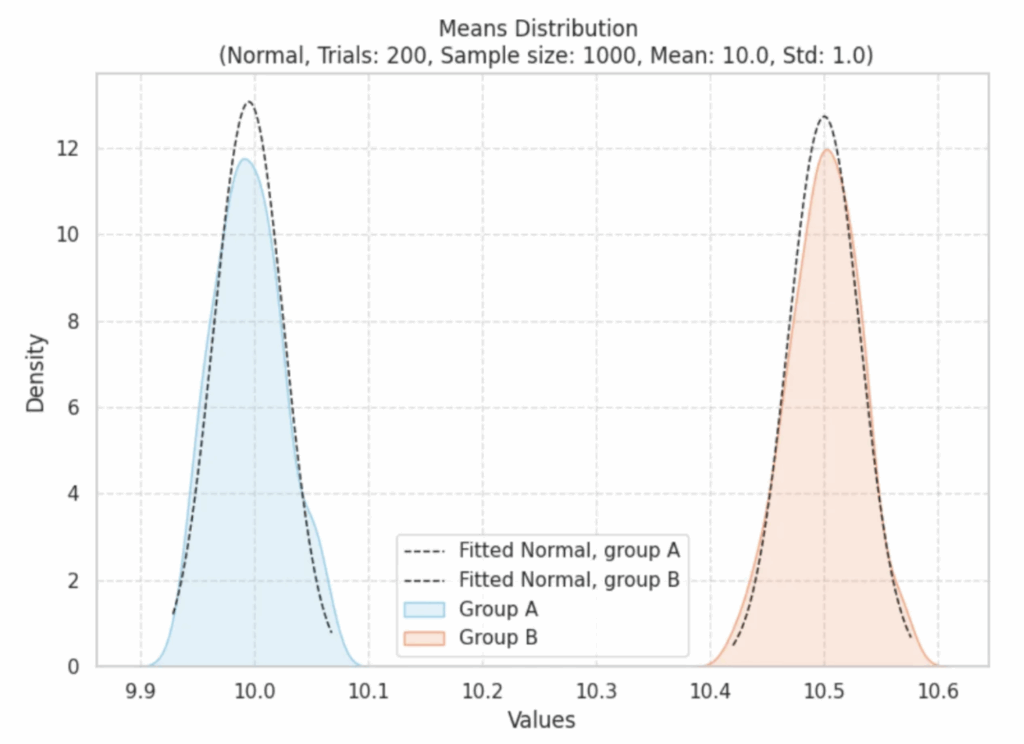
Распределение средних значений выборок
Согласно центральной предельной теореме, при выборке из генеральной совокупности распределение средних значений выборок будет стремиться к нормальному распределению. В наших наблюдениях мы явно это видим.
Теперь давайте проведем множество A/A- и A/B-тестов по логике, описанной выше.
- В A/A-тестах будем считать долю случаев, когда тест показывает статистически значимую разницу (хотя мы точно знаем, что ее нет). Тест работает корректно, если доля таких ошибок равна уровню значимости (α).
- В A/B-тестах будем считать долю случаев, когда тест обнаруживает разницу (которая действительно была нами добавлена). Этот показатель покажет нам мощность теста.
Результаты отобразим на графике: доля ложноположительных результатов A/A-тестов отмечена синим цветом, а доля истинно положительных результатов A/B-тестов — зеленым.
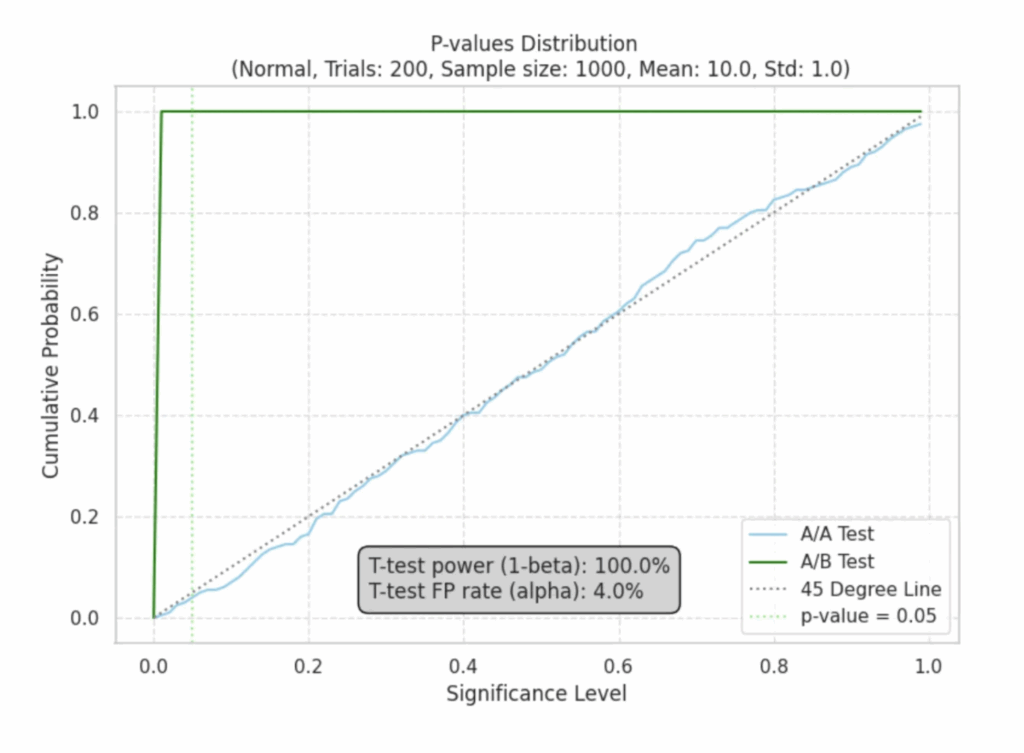
Синяя линия (A/A-тесты)
По оси X у нас указаны выбранные уровни значимости для теста (α), а по оси Y — процент статзначимых тестов.
Если статистический тест работает корректно, то для A/A-тестов (где разницы между группами нет) процент статзначимых тестов должен соответствовать уровню значимости. Это будет выглядеть как прямая под углом 45 градусов, означающая, что мы получаем ожидаемое количество ложноположительных тестов.
Конечно, в реальных условиях эта зависимость не будет идеально линейной — кривая может отклоняться из-за случайных факторов. Однако чем больше экспериментов, тем ближе она будет приближаться к идеальной прямой.
В нашем случае мы повторяем тест 200 раз, поэтому возможны небольшие отклонения из-за статистической погрешности.
Зеленая линия (A/B-тесты)
В A/B-тестах мы добавляем небольшой эффект (5%), поэтому здесь процент статзначимых тестов показывает, насколько хорошо тест выявляет реальную разницу. Если тест работает правильно, то процент значимых результатов должен соответствовать мощности теста (1 — β).
В идеале мы хотим, чтобы мощность теста была не ниже 80% — это значит, что тест способен выявить реальный эффект как минимум в 80% случаев. Поэтому зеленая линия должна быстро выходить на уровень 80% или даже выше. Если же зеленая линия остается ниже этого уровня, то тест слишком часто пропускает реальный эффект (это называется ошибкой II рода или ложноотрицательным результатом).
На графике выше мы наблюдаемая мощность теста быстро приближается к 100%.
Таким образом, t-тест ведет себя предсказуемо и надежно при данных, взятых из нормального распределения. Никаких сюрпризов!
Раскрытие интриги: за пределами нормальных распределений
Все становится еще интереснее, когда мы исследуем, как t-тест обрабатывает данные из других распределений. Рассмотрим одномодальное, логнормальное и половинное нормальное распределения.
Можно заметить, что в каждом случае оранжевое распределение выборочных средних смещено вправо ровно на те самые 5%, которые мы искусственно добавили для симуляции эффекта между группами в A/B-тесте. Напомню, ранее мы описывали, что для A/A-тестов выборки берутся из одинаковых распределений без добавления такого эффекта. Здесь же речь идет именно об A/B-тесте, где эффект присутствует по задумке.
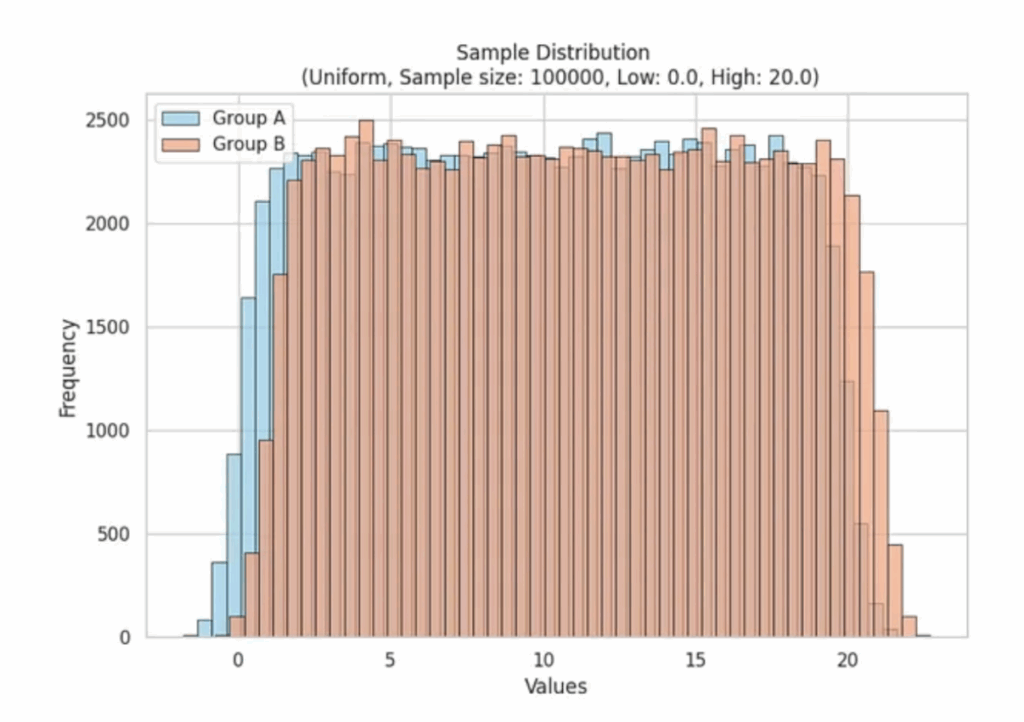
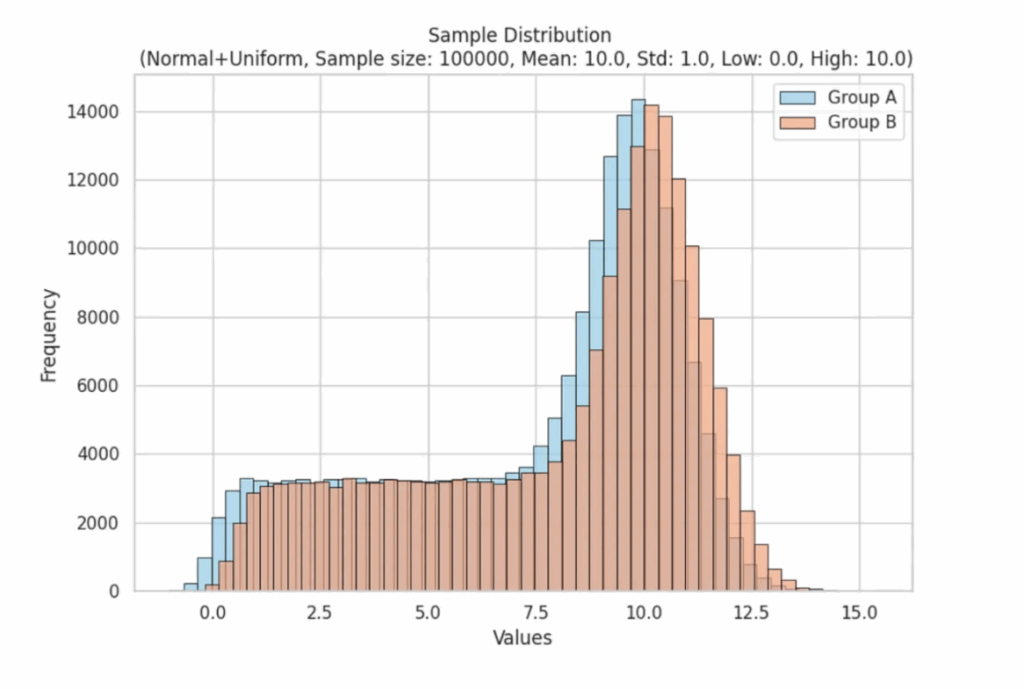
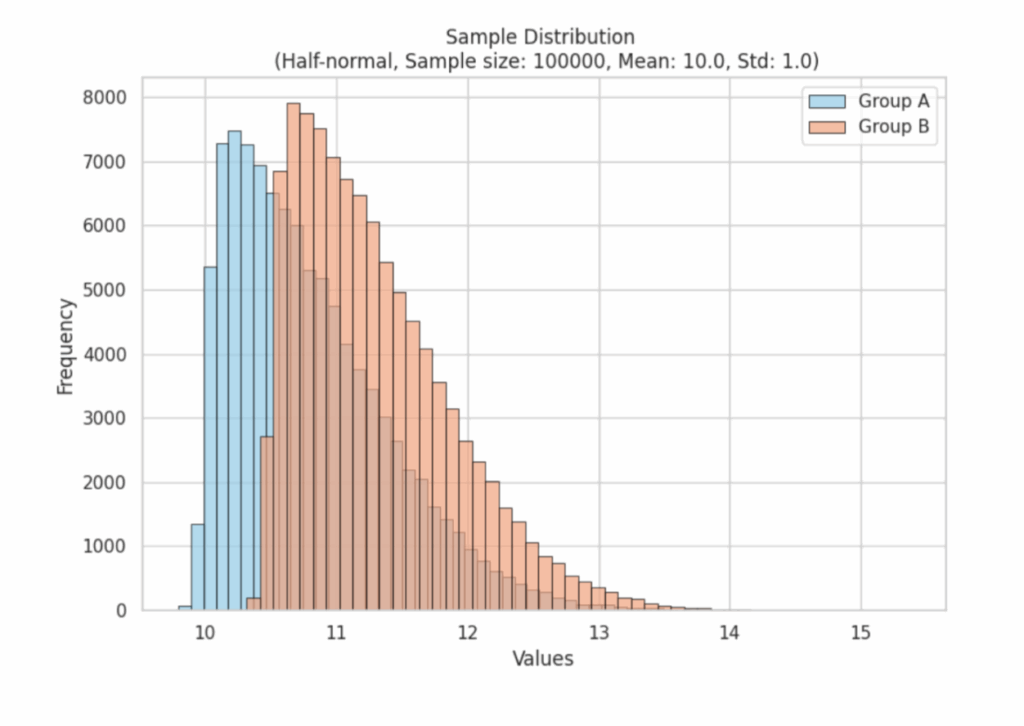
Распределение генеральных совокупностей для выборки
Наши первоначальные данные могут выглядеть как дикие, неупорядоченные. Возьмем, например, логнормальное распределение, которое имеет ярко выраженное смещение в сторону меньших значений.
После того как мы 200 раз возьмем 1000 значений для каждой группы и вычислим их средние, происходит замечательное преобразование. Распределение этих выборочных средних, даже для исходно смещенных данных, начинает напоминать знакомую колоколообразную кривую нормального распределения:
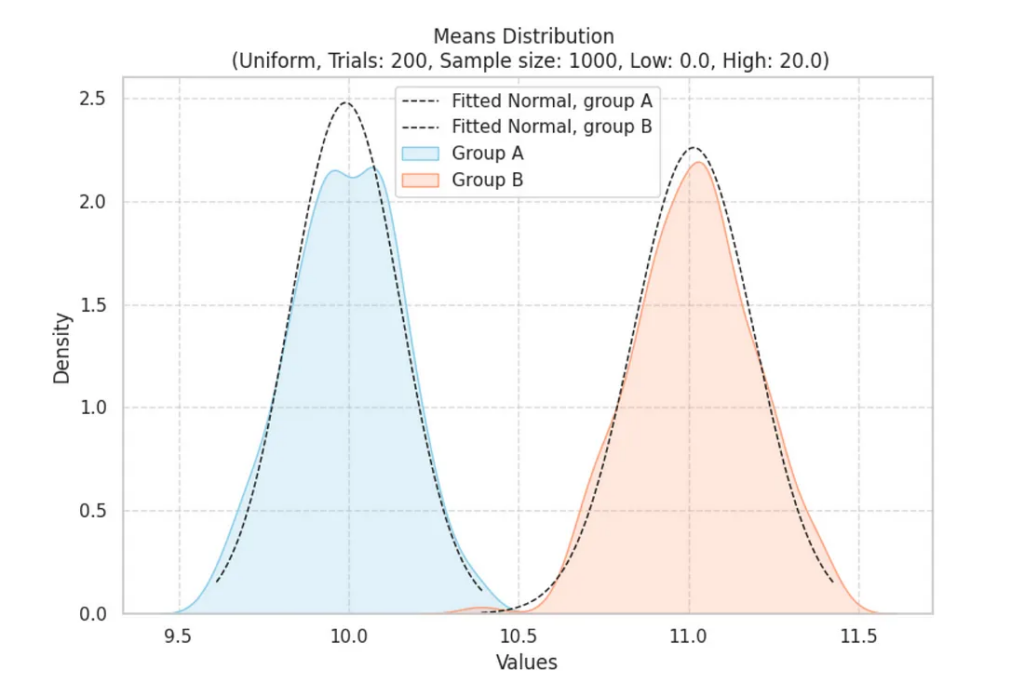
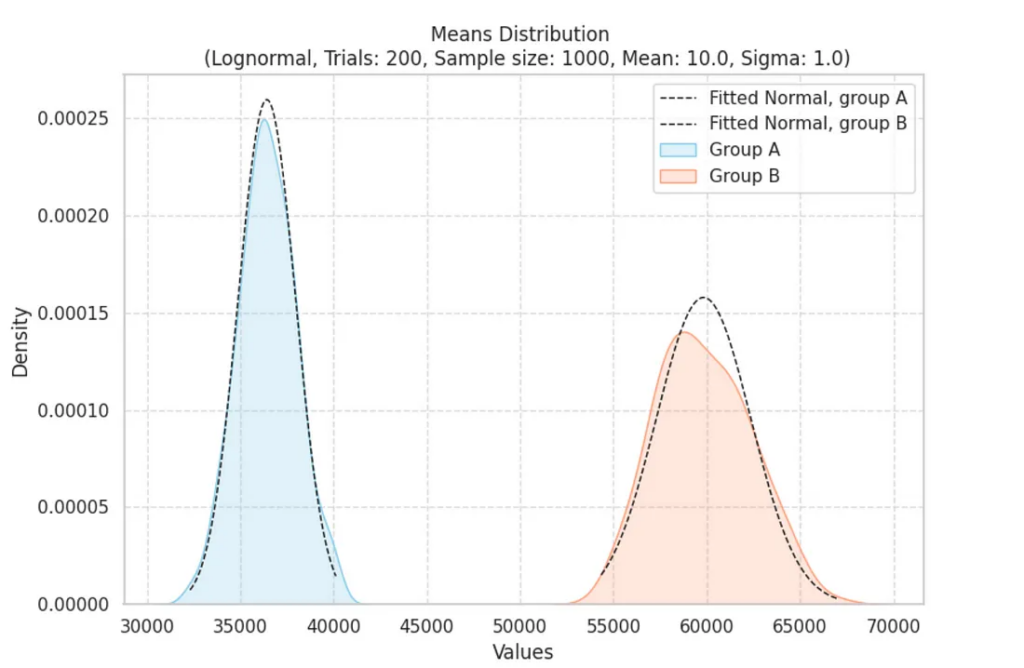
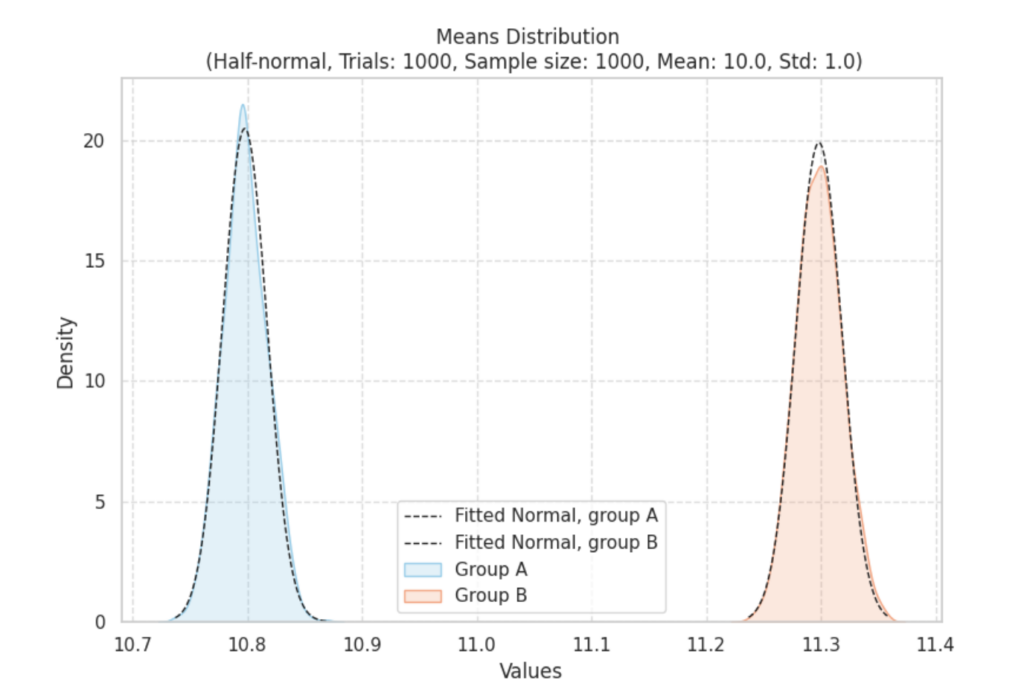
При проведении экспериментов t-тест демонстрирует удивительную надежность. Мы наблюдаем мощность выше 80%, что указывает на высокую вероятность обнаружения истинных различий между группами. Но самое главное, что уровень ложноположительных результатов остается низким: от 0% до 5% при пороговом значении p = 0.05. Это подчеркивает надежность t-теста даже при работе с не нормальными данными:
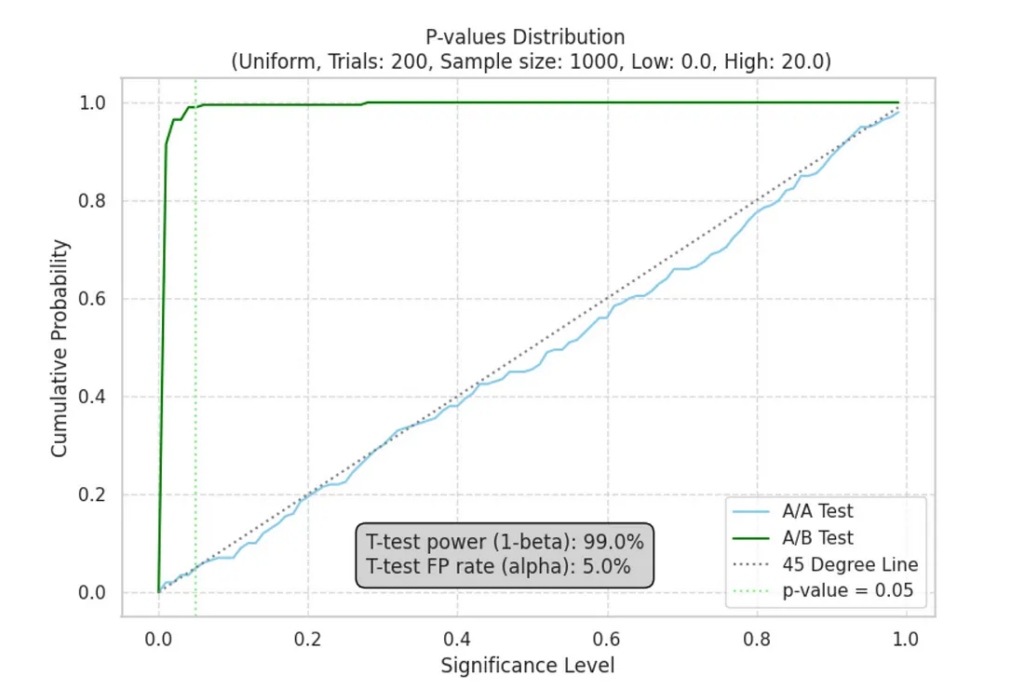
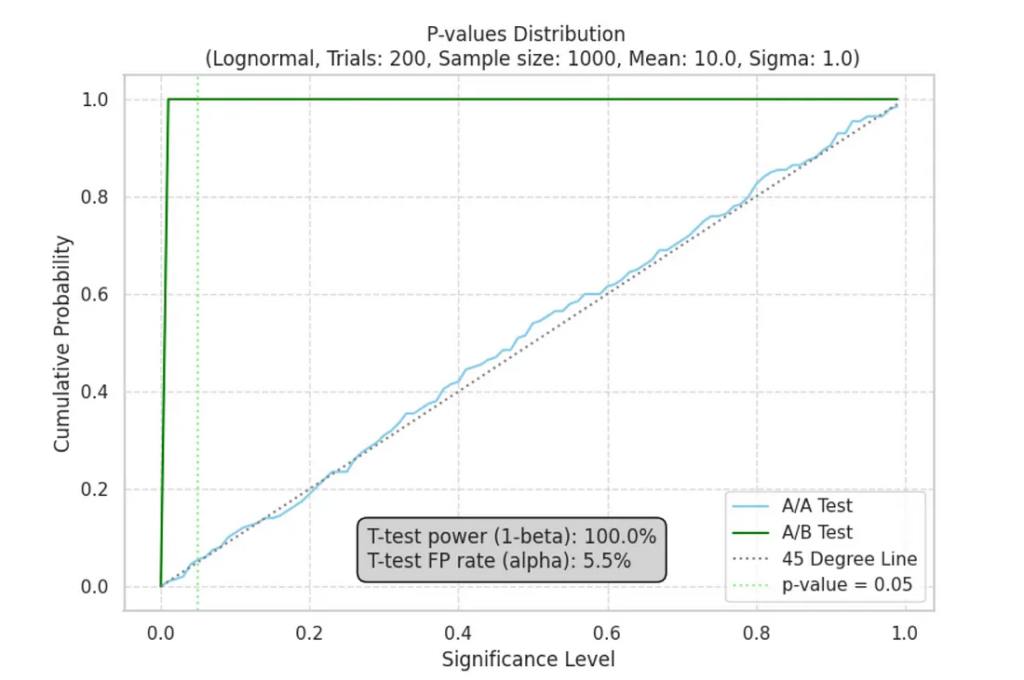
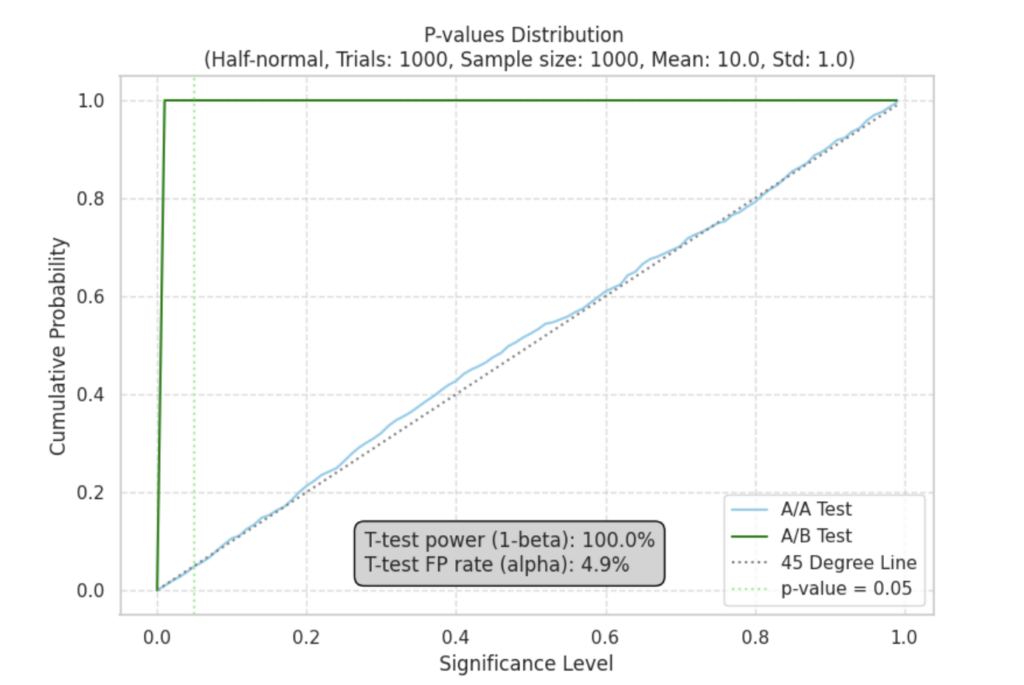
Алгоритм проверки статистического критерия для своих данных
Выше мы убедились, что t-test хорошо работает на ненормальных распределениях, но все же эти конкретные распределения не так часто встречаются в реальной жизни, тем более в продуктовой работе.
Давайте обсудим, как убедиться, что t-test или любой другой статистический критерий подходит для оценки результатов экспериментов на ваших специфичных данных.
Проверка на реальных данных
В качестве примера проверим критерий на реальных данных с выручкой интернет-магазина.
Такие данные обычно сильно перекошены, имеют большую дисперсию и чувствительны к «китам» (пользователям, которые делают покупки на большую сумму). В целом работа с денежными метриками — это одна из самых сложных задач при анализе A/B-тестов.
Давайте проверим, как с такими данными справится t-test.
У нас есть обезличенные данные интернет-магазина о сумме покупок за месяц. Данные сильно скошены влево и имеют длинный хвост с экстремальными значениями.
Это типичная картина для продуктовых метрик, связанных с деньгами: множество пользователей не совершают покупки вообще, большая часть покупателей делают небольшие покупки, но есть и небольшое количество «китов», которые тратят на покупки достаточно крупные суммы.
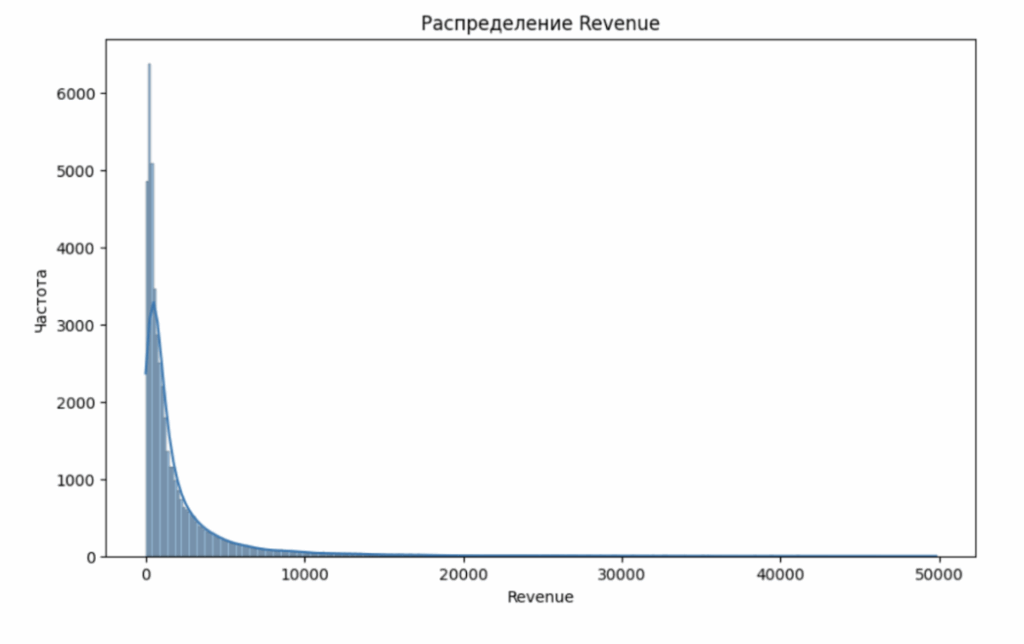
Всего у нас порядка 50 тысяч покупателей, среднее значение равно 3 тысячам, а максимальное значение — 668 тысяч. Стандартное отклонение — 14718.
Теперь возьмем выборку из 25 тысяч наблюдений. Разделим выборку на две группы, проведем A/A-тест. Далее группе Б увеличим revenue на 10% и проведем A/B-тест. Для каждой группы также посчитаем среднее. Повторим 1000 раз.
Конечно, это довольно сильное изменение, но оно подойдет для нашего исследования. В своих же исследованиях нужно ориентироваться на ожидаемый эффект от нововведений, которые вы обычно видите в своем продукте.
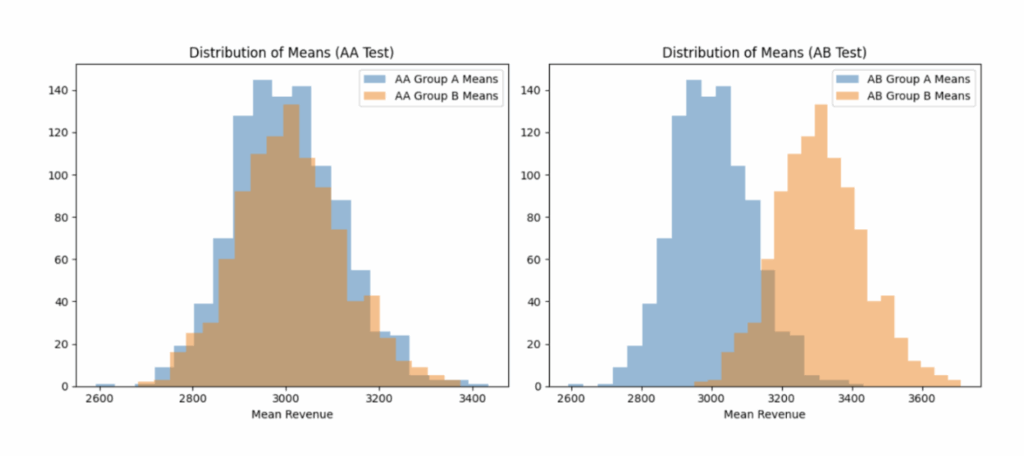
Как видим, наше распределение выборочных средних снова напоминает нормальное — все благодаря ЦПТ. А значит, есть все основания полагать, что t-тест отработает как полагается.
Теперь взглянем на распределение p-value:
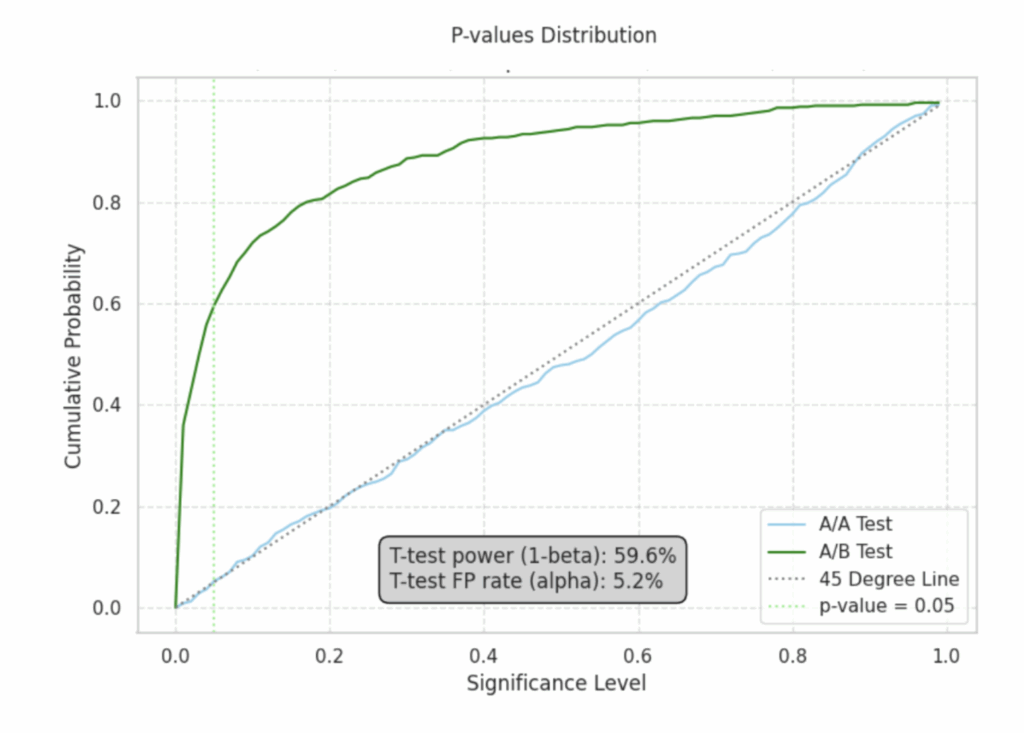
Кривая A/A-теста (синяя линия) располагается идеально под углом 45 градусов: это и есть наш показатель, что критерий можно применять на имеющихся данных. Критерий ошибается (говорит, что разница есть, когда ее нет) ровно столько, сколько должен.
Кривая A/B-теста также напоминает дугу, но в этот раз она довольно медленно приближается к 100%, что означает низкую мощность теста при маленьких значениях уровня значимости. Это значит, что тест будет часто говорить, что эффекта нет, хотя он есть.
Причина кроется в исходных данных с огромной дисперсией и экстремальными значениями. Представьте, что один из «китов» случайно попал в одну из групп. Это сразу сильно изменит средние значения соответствующей группы и может скрыть за собой те эффекты, которые мы пытаемся выловить из данных.
Есть несколько способов решить описанную проблему. Например, можно увеличить размер выборки или применить методы снижения дисперсии (применить CUPED или стратификацию). Но это лишь означает, что наш тест недостаточно чувствительный именно с выбранным размером выборки.
Увеличение размера выборки, продолжительности эксперимента или применение методов снижения дисперсии позволит постепенно повысить мощность теста. Если у вас есть возможность, рекомендуется отдельно проверить, как каждый из этих параметров влияет на мощность именно для ваших данных. Теперь вы знаете конкретный алгоритм для этого.
Можно повторить описанную выше процедуру симуляции, варьируя размер выборки или длительность теста, и наглядно увидеть, как это улучшает чувствительность теста и способность выявлять реальные эффекты.
При этом кривая A/A-теста гарантирует правильную (пусть и не самую мощную) работу t-теста на этих данных.
Заключение
Наше исследование демонстрирует устойчивость t-теста даже при наличии ненормальных данных. Центральная предельная теорема выступает в роли руководящего принципа, обеспечивая, что при выборке и расчете средних значений они будут стремиться к нормальному распределению, независимо от особенностей исходных данных.
Хотя мы рассмотрели крайние случаи и умеренный размер выборки, t-тест постоянно демонстрировал высокую мощность и низкий уровень ложноположительных результатов. Это подчеркивает его надежность как статистического инструмента для сравнения групп и получения значимых выводов.
В реальном мире анализа данных, где идеальная нормальность часто остается недостижимой целью, t-тест по-прежнему надежен и удобен в большинстве случаев. Однако, несмотря на общую устойчивость t-теста, перед его использованием всегда проверяйте, как он работает именно на ваших данных, используя подход с симуляцией, описанный выше. Это поможет понять, подходит ли он вам или стоит рассмотреть другие методы анализа.
Узнайте больше
— Почему ваши A/B-тесты требуют больше времени, чем могли бы
— Ухудшающие A/B-тесты — самый недооцененный инструмент менеджера продукта
Автор иллюстрации к материалу —










